☰ Browser-based graphics ⌫ Screen coordinate systems

Screen coordinate systems

To be able to draw anything on the screen we need to specify where the element will be placed. When working in 2D this placement is specified by giving two coordinates. Coordinates a numbers that help us make sense of space with a coordinate system. In this chapter we are going to look at two different coordinate systems, the cartesian system which we will use for rectangular 2D work and the polar system which we will use for circular screens or to make circular arrangements of our graphical elements.

Rectangular coordinates (aka 2D cartesian coordinates)

To be able to address pixels and set their color, a digital screen needs to know how to find them in the screen. All digital screens implement a coordinate system. This coordinate system is 2D, the horizontal position of a pixel is determined by the X coordinate and the vertical position by the Y coordinate. Therefore to know the position of a pixel on a screen we use two numbers (X, Y).

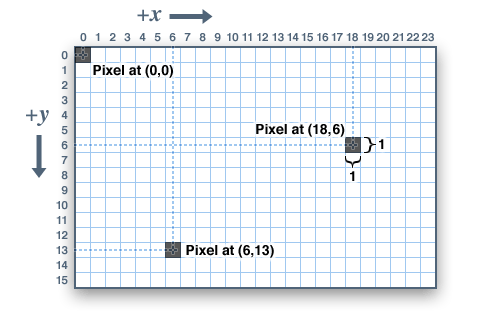
A single pixel is adimensional. We do not say that pixels have widths and heights by themselves, we think of them as single-dimensional dots. Shapes that are made of multiple pixels normally have a width and a height, such as for example a glyph in a typeface or a rectangle.

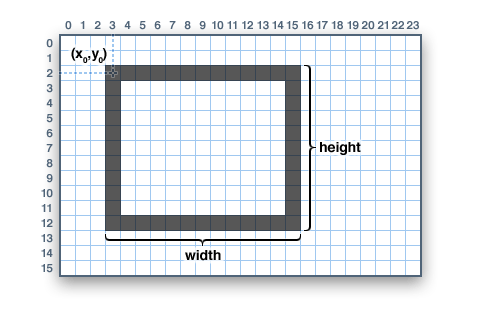
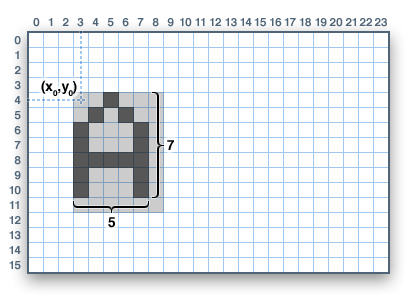
Compositional elements that have 0 or 1 as both their width and height are said to be degenerate and they are normally represented as a single pixel or culled completely from the scene. This is unimportant at this stage, but it is an important role in 3D graphics that aids in the optimization of the render process.

Click on this example canvas and move your mouse around to see the current coordinates of your mouse position.

Pixel address

Every pixel has an address, you can consider the address to be the place where that pixel is in memory or the ordinal of the pixel. The address can be calculated as: (y * width) + x. In most tools you will not need to use the address of the pixel. But it will be useful for generative graphics, shaders, and image filtering.

Relative coordinates

After a while of working with hand-calculated coordinates it gets annoying that to move your shape 50 pixels to the left, you have to substract 50 from it's x position. Isn't there a better way?

Sure there is! Developers are lazy people, they are always trying to make things easier for themselves, so when you observe that something is annoying and repetitive, someone else somewhere probably thought about it and there are other ways of doing things less tediously.

Become friends with push & pop

The push() and pop() functions of p5js can help us in handling our shapes and position them on screen without having to calculate the individual position of every coordinate for every shape.

Think of drawing in a p5js sketch as drawing with a pen that you can move around to different positions. The pen always begins at position 0, 0.

The push() function saves our current drawing state, including the current position of our pen. If after a push we do a translate(), it will save the pen position and then place the pen in the new position indicated by translate().

// our pen is at 0, 0
push(); // save our pen's state
translate(width/2, height/2); // move pen to center of screen
ellipse(0, 0, 10, 10); // draw ellipse at position 0, 0 relative to the current pen's position (center of screen)
pop(); // restore previous pen position

When you see a push() and pop() operation you can normally read it as "ok, this person is changing the frame of reference so that the (0,0) positions is somewhere else in the screen now".

This notion is quite important and it will come back later when we move to more advanced sketches, it is used quite heavily for animation and 3D.

Let's look at some practical examples of how this looks like:

Observe how the instruction that draws the ellipse hasn't changed at all, same parameters, yet these two circles are drawn at different positions. The trick is that the translate statement changes the origin of the coordinate system, what we put in translate(x, y) becomes our new (0,0).

The rotate() statement when given only one parameter will rotate our coordinate system by whatever angle we give it.

Let's draw the clock again using push(), pop(), translate(), and rotate().

At first it might seem boringly simple but push and pop have a hidden superpower in that they can be compounded, to create recursive visuals that can be visually quite complex.

Polar coordinate system

There's another way of using coordinates in 2D that is a little easier to use when we want to lay our graphical elements around a circle. It might sound like a crazy thing to do, but in graphics this actually happens very often. If you for example want to create symmetric shapes, you will often use this technique.

Polar coordinates are another way of specifying a position in two dimensional space based on how points are laid out in a circle. To know where in a circle a point is, all we need to know is an angle and the radius of the circle. Think about it for a moment.

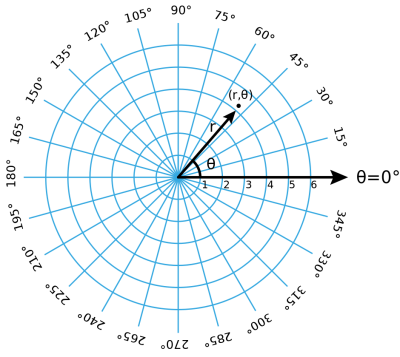
To specify the position of an element in polar coordinates, we need a radius that we will call r and an angle that we will call theta denoted by the greek letter θ.

Sometimes we want to draw something and then rotate slightly at an angle to draw another something, etc. And space these angles evenly, so that we get a symmetric pattern, all we then need to do is to increase the θ slightly every time we draw, to create this angular displacement. For example.

Drawing a clock

Let's draw 12 ellipses to denote the 12 positions of a clock's numbers. To do that we will increase our θ by a certain fixed amount every time ew draw an ellipse. That fixed amount is the total number of degrees in a circle, which is 360, divided by 12: 360 / 12 = 33. Our θ increment for every step is 33 degrees. And our radius always stays the same. So breaking down what we need to do into steps it's something like:

theta = 0
increment = 33

do 12 times:
  draw a circle at polar coordinate (r, theta)
  theta = theta + increment

Converting polar back to X and Y

Unfortunately p5js doesn't use polar coordinate, it uses cartesian coordinates, so before we draw our circle we need to convert polar coordinates back to cartesian.

The conversion involves a little bit of trigonometry, that part of maths where you use sinus and cosinus. It turns out the sinus of θ times the radius gives us the x position, and the cosinus of θ time the radius gives us the y position.

x = radius * sin(theta);
y = radius * cos(theta);

There's another thing that javascript doesn't do an therefore p5js doesn't do either and that's working with degrees. Using degrees to express angles is perhaps the most common way to think about it but computers often prefer radians, which is another way of expressing the same thing, only radians are expressed in relationship to PI which is a funny number we are not going to go into. This graphic shows how positions in a circle relate to radians. The only thing you need to know is that a full circle in radians is 2 * PI or TWO_PI in p5js.

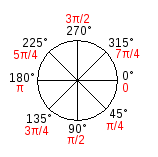
To better understand the relationship between trigonometric functions and the shape of a circle this Khan academy video does a pretty good job at showing it.

Follow the rabbit into the hole 🐰

• Read more about transformations in the Processing manual
• To better understand matrix transformations have a look at this one on matrix transformations